|
|
| Строка 1: |
Строка 1: |
| | {{DISPLAYTITLE:Информация о защитах выпускных квалификационных работ, 2012 год}} | | {{DISPLAYTITLE:Информация о защитах выпускных квалификационных работ, 2012 год}} |
| | | | |
| − | <!-- >
| + | <big><b>{{anchor|bachelors}}Выпускные работы бакалавров</b></big> |
| − | <big><b>{{anchor|courseworks}}Курсовые работы, 3‐й курс</b></big> | + | |
| | | | |
| | {{ВКР Инфо | | {{ВКР Инфо |
| | |name=Аминов Дмитрий Владимирович | | |name=Аминов Дмитрий Владимирович |
| − | |sciadvisor=Гвоздев Александр Александрович, доцент кафедры теор. физики, к. ф.‐м. н. | + | |sciadvisor=Гвоздев Александр Александрович, доцент кафедры теор. физики, д. ф.‐м. н. |
| − | |subj=Нерелятивистская заряженная частица в постоянном однородном магнитном поле | + | |subj=Релятивистский протон во внешнем постоянном магнитном поле |
| − | |abstract=:<i>В ходе данной работы решалось уравнение Шредингера для нерелятивистской частицы в постоянном однородном магнитном поле. | + | |abstract=:<i>Вычислена энергия и волновая функция релятивистского протона без аномального магнитного момента в постоянном однородном магнитном поле, исследовано уравнение Дирака для протона с аномальным магнитным моментом с целью нахождения его спектра энергии в магнитном поле. Получен спектр энергии и волновые функции для фермиона без аномального магнитного момента. Получен спектр энергии протона при наличии уnbsp;него аномального магнитного момента. Показано, что вnbsp;этом случае волновая функция протона не является собственной для оператора проекции спина на направление магнитного поля. Полученные выражения для спектра энергии протона вnbsp;однородном постоянном магнитном поле вnbsp;нерелятивистском пределе сводятся кnbsp;известным вnbsp;литературе выражениям.</i> |
| − | | + | |img=[[Файл:Aminov_D_V.jpg|180px|border|center|Аминов Дмитрий Владимирович]]}} |
| − | :В случае нерелятивистского электрона получены волновые функции и спектр энергии, зависящие от числа Ландау. Отмечено, что любое состояние (за исключением основного) двукратно вырождено по уровню Ландау и бесконечно вырождено по центру волнового пакета. В случае нерелятивистского протона получены волновые функции и спектр энергии, зависящий от числа Ландау и поляризации частицы.
| + | |
| − | | + | |
| − | :Отмечено, что наличие аномального магнитного момента снимает вырождение по числу Ландау, однако при этом волновая функция явно не зависит от аномального магнитного момента. Отмечено, что ширина расщепления уровня Ландау по поляризациям больше, чем расстояние между двумя соседними уровнями Ландау. Таким образом, в случае нерелятивистской частицы с большим аномальным магнитным моментом целесообразно выражать спектр энергии и волновые функции через осциляторное число и поляризацию.</i>
| + | |
| − | |img=[[Файл:No-image.gif|180px|center|]]|opq=on}} | + | |
| | | | |
| | {{ВКР Инфо | | {{ВКР Инфо |
| | |name=Блинова Анна Михайловна | | |name=Блинова Анна Михайловна |
| | |sciadvisor=Смирнов Александр Дмитриевич, профессор кафедры теор. физики, д. ф.‐м. н. | | |sciadvisor=Смирнов Александр Дмитриевич, профессор кафедры теор. физики, д. ф.‐м. н. |
| − | |subj=Плоские волны в теории неабелевого калибровочного поля | + | |subj=Рождение частиц в <span style="vertical-align:+0.9ex;"><math>e^+\,e^-</math></span>-столкновениях |
| − | |abstract=:<i>В ходе данной работы рассмотрены: группа SU(2); лагранжиан <math>\mathcal{L}=\partial_\mu\varphi^{+}\,\partial^\mu\varphi+m^2\,\varphi^{+}\varphi</math>, входящий в теорию двух комплексных скалярных полей, образующих дублет <math>\varphi(x)</math>, и инвариантный относительно глобальных преобразований, обладающий U(1)‐глобальной симметрией и фазой <math>\alpha</math>, не зависящей от координат; модифицированный лагранжиан, инвариантный относительно локальных преобразований SU(2), т. е. зависящих от точки пространства‐времени; тензор напряженностей <math>F_{\mu\nu}=\partial_\mu A_\nu-\partial_\nu A_\mu+\frac{g}{\mathrm{i}}\left[A_\mu,A_\nu\right]</math>; калибровочно‐инвариантный лагранжиан <math>\mathcal{L}_\mathrm{A}=-\frac{1}{2}\,\mathop{Sp}\left(F_{\mu\nu}\,F^{\mu\nu}\right)</math>, где <math>F^{i}_{\mu\nu}=\partial_\mu A^i_\nu-\partial_\nu A^i_\mu+g\,\varepsilon_{ijk}\,A^i_\mu\,A^k_\nu</math> и следующие из него уравнения без материи: <math>\left(D_\mu F^{\mu\nu}\right)^i=\partial_\mu F^{\mu\nu\,i}+g\,F^{\mu\nu\,k}\,\varepsilon_{ijk}\,A^i_\mu=0</math> и с материей: <math>\left(D_\mu F^{\mu\nu}\right)^i=g\,j^i_\nu</math>, а также уравнения Янга–Миллса для потенциалов.
| + | |abstract=:<i>Вычислены дифференциальные и полные сечения процесса рассеяния электрона на мюоне и процесса аннигиляции электрон-позитронной пары в мюон-антимюонную пару с учётом масс начальных и конечных частиц.</i> |
| − | | + | |img=[[Файл:Blinova_A_M.jpg|180px|border|center|Блинова Анна Михайловна]]}} |
| − | :Найдены решения уравнений Янга–Миллса в виде <math>A^i_\nu=A^i_\nu(\xi)</math>, где <math>\xi=n_\varsigma\,x^\varsigma=n^\varsigma\,x_\varsigma=x^0-\vec{n}\,\vec{x}</math> и <math>n^\sigma=(1,\vec{n})</math> — постоянный 4‐вектор. В частном случае <math>A^1_\mu(\xi)=A^2_\mu(\xi)=A^3_\mu(\xi)\equiv A_\mu(\xi)</math> найдено решение уравнений Янга–Миллса, при которых тензор напряженностей поля и уравнения Янга–Миллса переходят в соответствующие классические выражения электродинамики.
| + | |
| − | | + | |
| − | :Показано, что уравнения для неабелевого калибровочного поля в случае группы SU(2) допускают решения в виде плоских волн, соответствующие случаю абелевого калибровочного поля.</i>
| + | |
| − | |img=[[Файл:No-image.gif|180px|center|]]|opq=on}}
| + | |
| − | | + | |
| − | {{ВКР Инфо
| + | |
| − | |name=Дурандин Михаил Иванович
| + | |
| − | |sciadvisor=Кузнецов Александр Васильевич, профессор кафедры теор. физики, д. ф.‐м. н.
| + | |
| − | |subj=Дзета змееносца и её партнёр — история разрыва
| + | |
| − | |abstract=:<i>Звезда Дзета Змееносца относится к классу так называемых убегающих звёзд (runaway stars). Интерес к ней значительно усилился после обнародования снимка, сделанного инфракрасным телескопом WISE, на котором видно, как звезда проходит сквозь межзвёздное пространство, толкая перед собой и разогревая облако межзвёздной пыли и формируя ударную волну. Звезда обладает массой около 20 масс Солнца и видна невооружённым глазом. На данный момент её скорость оценивается на уровне 24 км/с. Столь большая скорость может свидетельствовать о том, что звезда в далёком прошлом была частью двойной системы. Взрыв её партнёра как сверхновой повлёк за собой изменение гравитационного взаимодействия, что и выбросило звезду в свободный полёт. Этот эффект называется эффектом пращи. На данный момент учёные нашли предполагаемого партнёра Дзеты Змееносца — это нейтронная звезда RX J185635-3754, являющаяся остатком взрыва сверхновой. | + | |
| − | | + | |
| − | :Задача курсовой работы состояла в анализе возможных траекторий движения звезды в гравитационном поле, создаваемом компактным остатком и облаком газа. Ввиду сложности полного динамического описания движения звезды использовалось приближение статического гравитационного поля. Распределение плотности в центральном компактном объекте было принято постоянным, распределение плотности облака газа — убывающим по степенному закону <math>c/r^{3+a}</math>, где <math>a</math> рассматривался как свободный параметр. Хотя размер облака в действительности является конечным, приближение бесконечного облака со степенным законом распределения плотности, с одной стороны, незначительно отличается от истинного распределения на небольших расстояниях от центра, с другой стороны, позволяет провести до конца аналитические вычисления.
| + | |
| − | | + | |
| − | :В зависимости от соотношения между массами компактного остатка и облака газа, с учётом различных значений параметра <math>a</math> и полного момента импульса системы был определён набор возможных траекторий движения звезды.
| + | |
| − | | + | |
| − | :Расширение задачи Кеплера на случай системы из компактного остатка и облака газа, в приближении статического гравитационного поля, позволяет определить аналитически виды траектории звезды путём анализа дифференциального уравнения движения. Для получения полного динамического описания движения звезды в изменяющемся со временем гравитационном поле требуется численный анализ дифференциального уравнения движения.</i>
| + | |
| − | |img=[[Файл:No-image.gif|180px|center|]]|opq=on}} | + | |
| | | | |
| | {{ВКР Инфо | | {{ВКР Инфо |
| | |name=Епихин Дмитрий Вячеславович | | |name=Епихин Дмитрий Вячеславович |
| | |sciadvisor=Кузнецов Владимир Степанович, доцент кафедры теор. физики, к. ф.‐м. н. | | |sciadvisor=Кузнецов Владимир Степанович, доцент кафедры теор. физики, к. ф.‐м. н. |
| − | |subj=Расчёт зонной структуры твердого тела | + | |subj=Спектр энергии электрона в квантовой точке |
| − | |abstract=:<i>В ходе данной работы были найдены собственные значения энергии электронов, движущихся в кристалле, которые свидетельствуют о наличии энергетических зон в кристаллических телах, т. е. энергетический спектр будет полосатым. Ширина полосы будет определяться обменным интегралом. | + | |abstract=:<i>Рассмотрена модель сферически симметричной полупроводниковой квантовой точки, в предположении, что электрон свободно движется внутри сферической ямы. Вычислены волновые функции электрона внутри квантовой точки и за её пределами. Показано, что волновые функции внутри квантовой точки выражаются через функции Бесселя полуцелого порядка, а вне квантовой точки через обобщенные полиномы Лагерра. Установлена зависимость вероятности нахождения электрона вне квантовой точки от ее размеров. Показано, что при увеличении размеров квантовой точки уменьшается вероятность нахождения электрона за её пределами.</i> |
| − | | + | |img=[[Файл:Epihin_D_V.jpg|180px|border|center|Епихин Дмитрий Вячеславович]]}} |
| − | :В методе приближения сильной связи было получено, что определенной атомной функции будет соответствовать своя полоса энергии и состояние электрона в полосе будет определяться значением квазиволнового вектора <span style="vertical-align:+0.9ex;"><math>\vec{k}</math></span>.
| + | |
| − | | + | |
| − | :Приближение сильно связанных электронов не описывает правильно с количественной точки зрения состояние электронов в зоне проводимости в реальных кристаллах. Поэтому это приближение не может быть использовано для количественных расчетов энергетического спектра и волновых функций электронов в конкретных кристаллах. Существенно, однако, то, что они дают хорошую иллюстрацию к общим выводам о движении электрона в периодическом поле.</i>
| + | |
| − | |img=[[Файл:No-image.gif|180px|center|]]|opq=on}} | + | |
| | | | |
| | {{ВКР Инфо | | {{ВКР Инфо |
| | |name=Следкова Полина Андреевна | | |name=Следкова Полина Андреевна |
| | |sciadvisor=Михеев Николай Владимирович, профессор, зав. кафедрой теор. физики, д. ф.‐м. н. | | |sciadvisor=Михеев Николай Владимирович, профессор, зав. кафедрой теор. физики, д. ф.‐м. н. |
| − | |subj=Дисперсия нейтрино с магнитном моментом в электромагнитном поле | + | |subj=Излучение электромагнитных волн магнитным моментом нейтрино |
| − | |abstract=:<i>В ходе данной работы получено уравнение Дирака и рассмотрены два случая: 1) при отсутствии электромагнитного поля; 2) с учётом электромагнитного поля. В первом случае были найдены значения энергии нейтрино. Во втором случае были найдены значения энергии нейтрино с учётом его магнитного момента в электромагнитном поле. Было показано, что в электрическом поле, т. е. <span style="vertical-align:+0.9ex;"><math>\vec{B}=0</math></span>, безразмерной величине <span style="vertical-align:+0.6ex;"><math>\alpha=\frac{\mu\,E}{m}</math></span>, определяющей значения энергии нейтрино, соответствует две возможные поляризации <span style="vertical-align:+0.4ex;"><math>\lambda=\pm 1</math></span>, что в свою очередь говорит о том, что нейтрино может находиться в двух состояниях со спином, направленным вдоль или против поля. | + | |abstract=:<i>В произвольном электромагнитном поле определена энергия нейтрино с учётом взаимодействия магнитного момента нейтрино с электромагнитным полем. Получено уравнение движения удвоенного среднего спина нейтрино. Получена оценка интенсивности электромагнитного излучения за счёт магнитного момента нейтрино.</i> |
| − | </i> | + | |img=[[Файл:Sledkova_P_A_2012.jpg|180px|border|center|Следкова Полина Андреевна]]}} |
| − | |img=[[Файл:Sledkova_P_A.jpg|180px|border|center|Следкова Полина Андреевна]]}} | + | |
| | | | |
| | {{ВКР Инфо | | {{ВКР Инфо |
| | |name=Шленев Денис Михайлович | | |name=Шленев Денис Михайлович |
| | |sciadvisor=Румянцев Дмитрий Александрович, доцент кафедры теор. физики, к. ф.‐м. н. | | |sciadvisor=Румянцев Дмитрий Александрович, доцент кафедры теор. физики, к. ф.‐м. н. |
| − | |subj=Электродинамика в веществе с учётом разложения по мультипольным моментам | + | |subj=Процесс резонансного рассеяния фотона на электроне с рождением пары нейтрино-антинейтрино |
| − | |abstract=:<i>Получены основные уравнения электродинамики в среде — уравнения Максвелла — с учётом вклада средних дипольного и квадрупольного моментов образца. Показано, что видоизменилось только одно из них в приближении пренебрежения излучением. Введён новый физический термин — понятие вектора квадрупольной поляризованности, который вошёл в формулы для скалярного потенциала поля, объёмной плотности связанных зарядов и вектора электрического смещения. Показано, что полученными поправками не следует пренебрегать только для тех немногих объектов, чей квадрупольный момент не является малой величиной по сравнению с дипольным. К ним с трудом можно отнести неполярные молекулы, поскольку, если даже их собственный дипольный момент равен нулю, он наводится при включении внешнего поля. Поэтому главным претендентом на роль такого объекта является квазичастица биэкситон, состоящая из двух дырок и двух электронов. | + | |abstract=:<i>Проведено исследование комптоноподобного процесса с рождением пары нейтрино-антинейтрино в сильно замагниченной плазме при резонансном случае. Плазма полагалась сильно вырожденной. Учтено, что в сильном поле электроны находятся на основном уровне Ландау. Вычислен элемент матрицы рассеяния, входящие в него амплитуды выражены через явные Лоренц-ковариантные структуры. Вычислено значение нейтринной светимости исследуемого процесса с учётом дисперсии фотона вnbsp;замагниченной плазме. Результат представим в виде четырёхкратного интеграла. Полученные результаты для амплитуд важны для расчёта квантовых процессов во внешнем постоянном однородном магнитном поле, когда заряженные частицы могут занимать произвольное количество уровней Ландау. Полученное выражение для светимости может вносить существенный вклад в изменение динамики остывания магнитаров, в которых возможно осуществление условий, необходимых для катализации данного процесса.</i> |
| − | | + | |img=[[Файл:Shlenev_D_M_2012.jpg|175px|border|center|Шленев Денис Михайлович]]}} |
| − | :Получена конфигурация поля однородно квадрупольно поляризованного шара. Показано, что внутри шара силовые линии поля — прямые, а вне шара линии поля имеют дипольный характер.</i>
| + | |
| − | |img=[[Файл:Shlenev_D_M.jpg|175px|border|center|Шленев Денис Михайлович]]}} | + | |
| | | | |
| | {{ВКР Инфо | | {{ВКР Инфо |
| | |name=Яргина Ксения Игоревна | | |name=Яргина Ксения Игоревна |
| | |sciadvisor=Пархоменко Александр Яковлевич, доцент кафедры теор. физики, к. ф.‐м. н. | | |sciadvisor=Пархоменко Александр Яковлевич, доцент кафедры теор. физики, к. ф.‐м. н. |
| − | |subj=Функция Грина в квантовой механике | + | |subj=Инварианты Ярлског |
| − | |abstract=:<i>Метод Швингера может быть использован для нахождения функции Грина уравнения Шрёдингера (в нерелятивистской квантовой механике) в картине Гейзенберга. Решения уравнений Гейзенберга позволяют выразить оператор Гамильтона через операторы координаты начального и конечного моментов времени, а его матричный элемент становится пропорциональным функции Грина. Уравнение Шрёдингера сводится к дифференциальному уравнению первого порядка по времени, для которого известно общее решение. Зависимость функции Грина от координат фиксируется начальными и граничными условиями. Данный метод применен для вычисления функций Грина свободной частицы и одномерного гармонического осциллятора. | + | |abstract=:<i>Рассмотрена матрица смешивания Кабиббо-Кобаяши-Маскава (ККМ) в стандартной модели с тремя и четырьмя поколениями. Приведены выражения для матрицы ККМ в стандартной параметризации и параметризации Вольфенштейна для 3 поколений, представлена процедура обобщения на случай четырех поколений. Рассмотрен инвариант Ярлског как параметр, не зависящий от выбора фаз кварковых полей, дана его геометрическая интерпретация в виде «треугольников унитарности». Рассмотрено обобщение инварианта Ярлског на случай четырех поколений фермионов.</i> |
| − | | + | |img=[[Файл:Yargina_K_I_2012.jpg|180px|border|center|Яргина Ксения Игоревна]]}} |
| − | :В работе произведено вычисление функции Грина временного уравнения Шредингера для свободной частицы и одномерного осциллятора.</i>
| + | |
| − | |img=[[Файл:Yargina_K_I.jpg|180px|border|center|Яргина Ксения Игоревна]]}}
| + | |
| − | | + | |
| − | ---- | + | |
| − | <big><b>{{anchor|bachelors}}Выпускные работы бакалавров</b></big>
| + | |
| − | | + | |
| − | {{ВКР Инфо
| + | |
| − | |name=Беляев Василий Андреевич
| + | |
| − | |sciadvisor=Гвоздев Александр Александрович, доцент кафедры теор. физики, к. ф.‐м. н.
| + | |
| − | |subj=Уравнение состояния вырожденного кваркового газа
| + | |
| − | |abstract=:<i>В работе произведено вычисление уравнения состояния вырожденной кварковой материи в модели мешка с учётом массы s‐кварка и магнитного поля. В работе были исследованы среды, состоящие из (u,d) и (u,d,s)‐кварков, на предмет стабильности, далее вычислены концентрации массивных кварков и ультрарелятивистских электронов в магнитном поле, а также уравнение состояния вырожденного кваркового газа в модели мешка с учётом массы s‐кварка и магнитного поля.
| + | |
| − | | + | |
| − | :В результате исследования было показано, что в простейшей модели кваркового мешка стабильной является странная кварковая среда (система из u‐, d‐, s‐кварков с глюонным натяжением и электронов). Для этой системы получено уравнение состояния странной кварковой материи в магнитном поле. Численная оценка поправок, связанных с влиянием магнитного поля, показывает, что этими поправками можно пренебречь при характерных параметрах сверхплотного состояния кварковой среды (химическом потенциале μ = 500 МэВ, массе s‐кварка m<sub>s</sub> = 100 МэВ) и напряжённостях сверхсильного магнитного поля 2·10<sup>16</sup> ≤ B ≤ 4·10<sup>17</sup> Гс.</i>
| + | |
| − | |img=[[Файл:Belyaev_V_A.jpg|180px|border|center|Беляев Василий Андреевич]]}}
| + | |
| − | | + | |
| − | {{ВКР Инфо
| + | |
| − | |name=Мазалецкий Леонид Алексеевич
| + | |
| − | |sciadvisor=Смирнов Александр Дмитриевич, профессор кафедры теор. физики, д. ф.‐м. н.
| + | |
| − | |subj=Рождение пар частиц в e<sup>+</sup> e<sup>-</sup>‐столкновениях
| + | |
| − | |abstract=:<i>Основным способом изучения свойств фундаментальных свойств частиц является исследование результатов их столкновений на современных коллайдерах. В последние десятилетия основные результаты были получены с е<sup>+</sup>е<sup>-</sup>‐коллайдера LEP, с коллайдера Теватрон, в ближайшем будущем предстоит выполнить большую программу исследований на Большом Адроном Коллайдере LHC, на котором будут получены новые данные об особенностях взаимодействия кварков и лептонов при высоких энергиях. При проведении о объяснении получаемых результатов в первую очередь необходимо знание сечения рождения изучаемых частиц.
| + | |
| − | | + | |
| − | :В настоящей работе рассматривается простейший случай рассеяния электрона на мюоне. В работе в рамках Стандартной модели электрослабого взаимодействия вычисляются и анализируются дифференциальные и полные сечения рассеяния и аннигиляци.
| + | |
| − | | + | |
| − | :В ходе проделанной работы было проведено ознакомление с правилами построения амплитуд рассеяния диаграммной техники Фейнмана. Было показано, что в системе центра инерции при условии, что род частиц в процессе реакции не изменяется, импульсы начальные совпадают с конечными. Посчитано дифференциальное сечение рассеяния электрона на мюоне.</i>
| + | |
| − | |img=[[Файл:Mazaletskiy_L_A.jpg|180px|border|center|Мазалецкий Леонид Алексеевич]]}}
| + | |
| − | | + | |
| − | {{ВКР Инфо
| + | |
| − | |name=Мосичкин Анатолий Фёдорович
| + | |
| − | |sciadvisor=Кузнецов Владимир Степанович, доцент кафедры теор. физики, к. ф.‐м. н.
| + | |
| − | |subj=Процессы самоорганизации в полупроводниках в сильном электрическом поле
| + | |
| − | |abstract=:<i>В работе исследовано коллективное поведение носителей заряда и токовых неустойчивостей в собственном полупроводнике при учёте процессов тепловой и фотогенерации, излучательной рекомбинации, ударной ионизации и Оже‐рекомбинации. Выполнен теоретический расчёт вольт‐амперной характеристики кремниевого полупроводника заданной длины. Проведён теоретический расчёт зависимости критического тока в полупроводнике от величины электрического поля. Найдено распределение концентрации электронов и дырок в кремниевом полупроводнике в области электрических полей, близких к полю пробоя.
| + | |
| − | | + | |
| − | :Получены три возможных варианта распределения концентрации носителей заряда в полупроводнике. В одном из случаев концентрация дырок убывает в направлении электрического поля, а концентрация электронов возрастает. Выяснено, что вольт‐амперные характеристики в случае сильных и слабых токов практически совпадают.</i>
| + | |
| − | |img=[[Файл:Mosichkin_A_F.jpg|180px|border|center|Мосичкин Анатолий Фёдорович]]}}
| + | |
| − | | + | |
| − | {{ВКР Инфо
| + | |
| − | |name=Радченко Мария Сергеевна
| + | |
| − | |sciadvisor=Кузнецов Александр Васильевич, профессор кафедры теор. физики, д. ф.‐м. н.
| + | |
| − | |subj=Квантовые алгоритмы для трудно решаемых задач
| + | |
| − | |abstract=:<i>В работе исследованы типы трудно решаемых задач с использованием квантовых вычислений, выполнено построение алгоритмов для их решения, сделана оценка их вычислительной сложности с ростом входных данных, возможности реализации этих алгоритмов на простейших ЯМР — компьютерах.
| + | |
| − | | + | |
| − | :Квантовомеханические эффекты, такие как экспоненциальность пространства состояний, перепутанные состояния или когерентная суперпозиция, которая в общем случае не имеет классических аналогов, линейность преобразований квантовых состояний — именно эти эффекты делают возможным квантовый параллелизм. С помощью него возможна реализация сразу нескольких математических операций, всего лишь за одно обращение к «чёрному ящику», что и даёт нам экспоненциальное превосходство квантовых алгоритмов над классическими. Несмотря на то, что квантовые вычисления должны быть линейны и обратимы, любой классический алгоритм также может быть реализован на квантовом компьютере. Алгоритм Дойча показал, что данную задачу можно решить экспоненциально быстрее с помощью квантовых эффектов, чем с помощью классических средств. В случае классического компьютера задача поиска в неструктурированной базе данных занимает в среднем N/2 шагов, а алгоритм Гровера, использующий свойство квантового параллелизма, способен произвести данную операцию за <span style="vertical-align:+0.9ex;"><math>\sqrt{N}</math></span> шагов. Одно из возможных применений этого алгоритма — взлом криптографических систем, таких как DES. Алгоритм Шора даёт метод факторизации целого числа N за время полиномиальное (менее, чем с кубической зависимостью) в зависимости от входных данных. В данном случае квантовое преобразование Фурье не ускоряет вычисление, но позволяет при определённых условиях найти хорошие приближения для собственных чисел унитарного оператора. Это и позволяет решать задачу факторизации. Кроме того, трудновыполнимость факторизации лежит в основе наиболее надёжных на сегодняшний день классических методов шифрования, в частности системы и решение данной задачи, ставит под угрозу все классические криптографические системы защиты.
| + | |
| − | | + | |
| − | :Несмотря на огромное преимущество квантовых вычислений, есть недостатки, которые до сих пор не могут быть решены. Как известно, любой компьютер, в том числе и квантовый, оперирует некоторым набором базовых логических элементов. Квантовые логические элементы отличаются от их классических аналогов тем, что они могут создавать квантовые суперпозиции и производить операции над ними. Следовательно, чем больше у нас будет взаимодействующих кубитов, тем труднее будет разобрать взаимодействие, при котором проявляется квантовая интерференция. Ещё одной из наиболее серьёзных проблем является предотвращение влияния взаимодействия, обеспечивающего квантовую интерференцию, на окружающую среду. Чем больше используется компонентов, тем с большей вероятностью квантовая информация распространится за пределы квантового компьютера и будет потеряна во внешней среде, таким образом, искажая вычисления.</i>
| + | |
| − | |img=[[Файл:Radchenko_M_S.jpg|180px|border|center|Радченко Мария Сергеевна]]}}
| + | |
| − | | + | |
| − | {{ВКР Инфо
| + | |
| − | |name=Русов Алексей Валерьевич
| + | |
| − | |sciadvisor=Пархоменко Александр Яковлевич, доцент кафедры теор. физики, к. ф.‐м. н.
| + | |
| − | |subj=Константа распада В‐мезона из правил сумм КХД
| + | |
| − | |abstract=:<i>В настоящее время значение константы распада B‐мезона f<sub>B</sub> экспериментально извлекается из относительной вероятности распада B<sup>+</sup> → τ<sup>+</sup> ν<sub>τ</sub>. Полученная оценка превосходит имеющиеся теоретические предсказания. В недавней работе Ву и др. была проанализирована чувствительность константы распада к выбору интерполяционного тока и, в частности, было показано, что при использовании кирального тока значение f<sub>B</sub> заметно увеличивается. Данный анализ проводился методом правил сумм КХД, в рамках которого была выявлена существенная зависимость от величины массы b‐кварка.
| + | |
| − | | + | |
| − | :В данной работе на основе дальнейшего обобщения интерполяционного тока B‐мезона посредством параметризации векторной части произвольной константой <math>a</math> построены правила сумм КХД для константы распада f<sub>B</sub>. Метод правил сумм КХД разобран на примере вычисления пертурбативной части соответствующего коррелятора. Получена зависимость константы распада f<sub>B</sub> от параметра <math>a</math>. Проведено сравнение с феноменологическим значением f<sub>B</sub> и показано, что векторная часть должна существенно доминировать в интерполяционном токе, так как численно <math>a</math> ∼ 7. Представляется интересным провести подобный анализ правил сумм при учете непертурбативных эффектов, которые включаются в виде членов, содержащих вакуумные конденсаты кварковых и глюонных полей.</i>
| + | |
| − | |img=[[Файл:Rusov_A_V.jpg|180px|border|center|Русов Алексей Валерьевич]]}}
| + | |
| − | | + | |
| − | {{ВКР Инфо
| + | |
| − | |name=Шилова Наталья Сергеевна
| + | |
| − | |sciadvisor=Кузнецов Владимир Степанович, доцент кафедры теор. физики, к. ф.‐м. н.
| + | |
| − | |subj=Квазистационарные состояния в квантовой механике
| + | |
| − | |abstract=:<i>В работе проведено рассмотрение туннельного эффекта в квантовой механике. Найден коэффициент прохождения частицы через потенциальную яму и одномерный потенциальный барьер. Изучены квазистационарные состояния в квантовой механике. Вычисление времени жизни частицы в этом состоянии.
| + | |
| − | | + | |
| − | :В ходе решения первой задачи было выяснено, что прохождение частицы через потенциальный барьер возможно, если энергия частицы меньше высоты барьера.
| + | |
| − | | + | |
| − | :Во второй задаче было получено, что при увеличении энергии коэффициент прохождения стремится к 1. Это значит, что почти все частицы проходят над ямой. Внутри ямы имеет место осциллирующее решение, чем глубже яма, тем больше осцилляции, а вне ямы волновая функция «просачивается» наружу. А с ростом глубины ямы, число уровней энергии и связанных состояний будет увеличиваться, а вероятность обнаружения частицы внутри ямы будет становиться все меньше, а при стремлении в глубины ямы в бесконечность она обратится в ноль. Число уровней всегда конечно и определяется глубиной и шириной потенциальной ямы.
| + | |
| − | | + | |
| − | :В третьей задаче получили, что чем выше уровни энергии над ямой, тем меньше время жизни частицы на этом уровне.</i>
| + | |
| − | |img=[[Файл:Shilova_N_S.jpg|180px|border|center|Шилова Наталья Сергеевна]]}} | + | |
| − | </ -->
| + | |
| | | | |
| | ---- | | ---- |
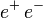-столкновениях».
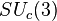до группы киральной цветовой симметрии 
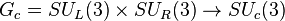, которая предполагается точной при некоторых относительно высоких энергиях и нарушенной до группы 
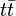-пар в 
-, 
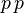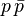-столкновениях при энергиях Тэватрона и Большого Адронного Коллайдера (БАК).
